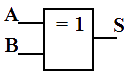
La logique combinatoire permet la création de système avec des porte logique à partir d’une équation logique.
Pour parler de système logique, il faut que la sortie dépende uniquement de l’entrée.
En logique combinatoire, les données traitées sont en généralement en binaire. Les variables ont donc deux états :
– l’état haut 1
– l’état bas 0
Les portes logiques
Pour bien réussir en SIN1 il faut connaitre les représentations et le fonctionnement des portes logiques les plus courantes.
Les portes logiques ont souvent deux représentations qui correspondent chacune à une norme différente.
Le fonctionnement de chaque fonction est représenté par un tableau appelé table de vérité. Celui-ci donne la valeur de la sortie suivant toutes les combinaisons possibles d’entrée.
La porte ET
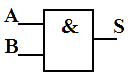

Elle correspond à l’opérateur et qui a pour signe « . »
Table de vérité
| B | A | Sortie |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pour comprendre ce que cela représente on peut représenter cette porte par un schéma électrique
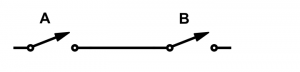
Ici les entrées sont représentées par des interrupteurs. Quand A=0, il est ouvert sinon il est fermé (A=1).
La fonction ET correspond à la mise en série de plusieurs interrupteurs, on voit que le seul cas pour que le courant passe est quand A=1 et B=1.
La porte OU


Elle correspond à l’opérateur et qui a pour signe « + »
Table de vérité
| B | A | Sortie |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Schéma électrique
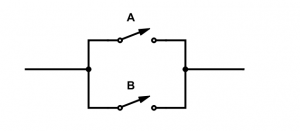
La fonction ET correspond à la mise en parallèle de plusieurs interrupteurs, on voit que le seul cas pour que le courant ne passe pas est quand A=0 et B=0.
La porte XOR
Elle correspond à l’opérateur et qui a pour signe « ⊕ »
Equation: A ⊕ B = (A./B)+(/A.B)
Table de vérité
| B | A | Sortie |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Schéma électrique
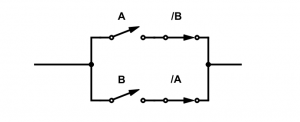
On représente ici la XOR à partir de l’équation logique (A./B)+(/A.B) on voit que les seul cas où le courant ne passe pas sont : A=0 et B=0
A=1 et B=1
Porte inverseuse
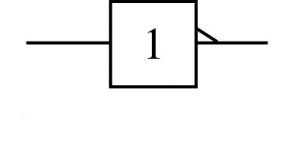
On peut inverser une équation grâce à une porte inverseuse. De plus il existe déjà de portes logiques déjà inversé, elles sont représentées par le même schéma suivis d’un petit rond.
Méthode TP
En TP il faudra être capable de passer d’une équation logique au câblage de celle-ci sur la platine. Pour cela on suit ces étapes.
- Extraire l’équation logique du sujet ou d’une table de vérité
- Simplifier le plus possible l’équation avec un tableau de Karnaugh
- Faire le schéma de l’équation simplifié
- Câblé sur la platine
Il est parfois nécessaire de modifier l’équation en prenant en compte le nombre de porte logique disponible sur la platine. De plus seul la porte NAND possède 3 entrées.
- Pour extraire une équation d’un problème posé à l’écris le plus simple est de faire la table de vérité correspondant au sujet. Pour cela on identifie d’abord les entrées puis on énumère chaque cas.
- On les regroupe ensuite dans ne table de vérité puis on vérifie si il n’y a pas d’incohérence.
- On utilise un tableau de Karnaugh pour réduire l’équation pour qu’elle soit plus simple à câblé.
- Si on veut modifier l’équation obtenue pour changer les portes utilisées on utilise cette méthode :
- a) on inverse tous les termes (on met une barre dessus)
- b) on change les opérateur (on remplace les + par des . et inversement)
- c) on inverse l’équation complète (on met une barre sur toute l’équation)
- exemple : (/a.b)+(a./c) on souhaite utilisé des NAND
- a) /(/a.b)+/(a./c) ici on considère (/a.b) et (a./c) comme un seul terme
- b) /(/a.b)./(a./c)
- c) /(/(/a.b)./(a./c))
- Pour faire le schéma on met les entrées à gauche et on place les portes logiques de l’équation les unes à la suite des autres suivant les parenthèses
- On câble sur cette platine en suivant pas à pas notre schéma.