L’Energie en soit ce n’est pas si compliqué, il vous suffit de comprendre le font du cours et le tour est joué ! Sinon pas de panique il existe trois méthodes pour résoudre un même exercice et cela marche tout le temps.
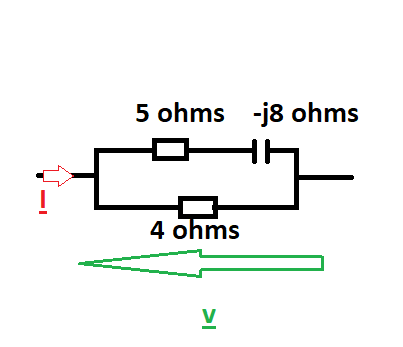
|Le but de cet exercice est de trouver la valeur de I
P.S: R1=5 ohms ; R2=4 ohms ; X = -j8 ohms ; V=94 V ; V origine des phases
->Première méthode : Les complexes
Rappel de cours : Zr= R ; ZL = jLw ; Zc=1/jCw ; V= I x Ztot
Tout d’abord nous allons commencer par exprimer les impédances équivalentes :
Zeq1= Zr1 + Zc =R1+ (1/jCw)
Ztot= Zeq1 // Zr2
Ztot=(Zr2 x Zeq1)/(Zr2 + Zeq1)
Je vous sens vouloir partir dans des calculs fastidieux mais ici ce n’est pas la peine, on a directement les valeurs des différentes impédances !!! Il suffit de remplacer par les valeurs.
Lisez attentivement et allez au plus simple !
Ztot= (4 x (5- 8j))/(4+ 5- 8j)
Ztot = (20 -32j )/(9- 8j )
De là deux choix s’offrent à vous :
- Soit on développe pour retirer la partie complexe du dénominateur et ainsi obtenir une solution plus simple à étudier
- Soit on a peur de faire des erreurs de signe et on passe le numérateur en polaire ainsi que le dénominateur. Comme suit :
Pour passer en coordonnées polaires il faut taper à la calculatrice : « seconde », « + » et on écrit
pol( Partie réelle ; Partie imaginaire)
Ce qui nous donne après coups :
20-32j -> pol(20;-32) -> [37,73 ; -57,9°]
9-8j -> pol(9;-8) -> [12,04 ; -41,63°]
Ztot= [37,73 ; -57,9°]/ [ 12,04 ; -41,63°]
Ztot= [3,13 ; -16,27°]
Petit rappel : Sous forme de fraction, les impédances se divisent et les phases se soustraient c’est-à-dire on fait -> (numérateur – dénominateur) . Sous forme de multiplication les impédances se multiplient et les phase se somment.
Comme rappelé plus haut V=I x Ztot
On a alors :
I=V/Ztot
I= 94/ [3,13; -16,27°]
I=[30 ; + 16,27°]
On a alors trouvé par la méthode des complexes que I = 30 A.
|Seconde méthode : Les puissances
Elle utilise le théorème le plus adulé des élèves, j’ai nommé : Le théorème de Boucherot
Petit rappel : R1= 5 ohms ; R2= 4 ohms ; X = -8j ohms S= U x I = racine(P²+Q²)
La puissance active est nulle dans le cas d’une charge L ou C pure et la puissance réactive est nulle dans le cas d’une charge résistive pure.
Ptot= Pr1 + Pr2
Pr2 = (V²/R2) = 94²/4 = 2209 W
I1 = V/ (Zr1+Zc) = V/module(Z) = 94/ racine(5²+8²)= 9,96 A
Pr1= R x I1² = 5 x 9,96² = 496 W
-> Ptot = 496 + 2209 = 2705 W
Ici nous avons d’abord calculé la branche la plus simple c’es-à-dire avec R2 puis nous avons calculé le courant contenu dans la première branche car on a un dipôle complexe composé d’une résistance et d’un condensateur on en a besoin pour calculer la puissance active et réactive.
Q= -X x I1² = -8 x 9,96² = -794 VAR Ainsi S=racine(Ptot² + Q²) = racine( 2705² + (-794)²) S= 2819 VA -> I = S/V = 2819 / 94 = 30 A
Nous avons encore prouvé de façon plus rapide qu’il était que I= 30 A .
Troisième méthode : Repère de Fresnel
Celle ci est la moins comprise des élèves et pourtant elle n’a rien de compliqué. Ce ne sont que des applications de vecteurs et des produits en croix. Il faut d’abord faire quelques petits calculs : On va calculer le courant qui se trouve dans la première branche puis dans la seconde :
I1 = V/ module(Z) = 94 / racine(5²+8²) = 9,96 A I2 = V/R = 94 / 4 = 23,5 A Phase1: pol(5;-8) -> [9,43; -57,9°]

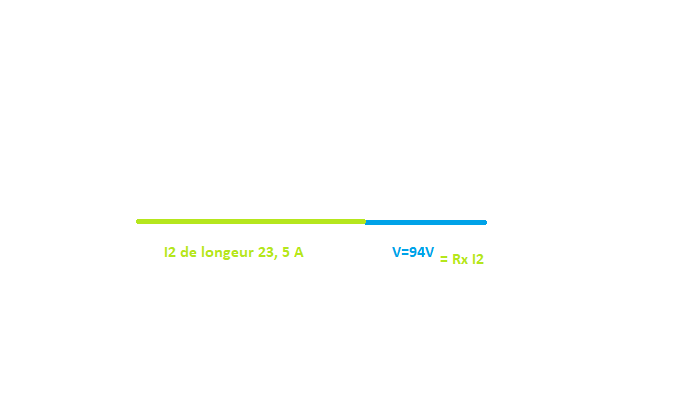
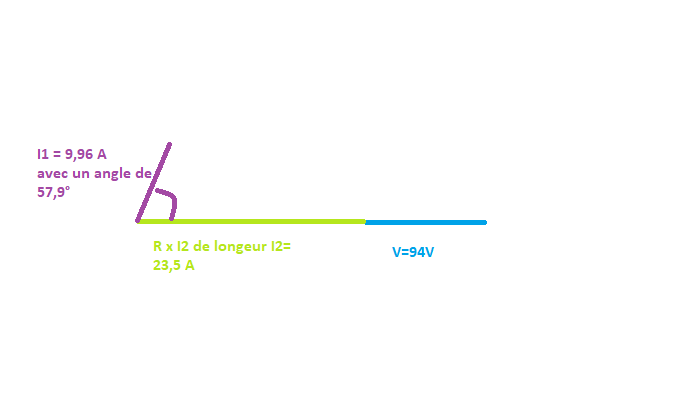
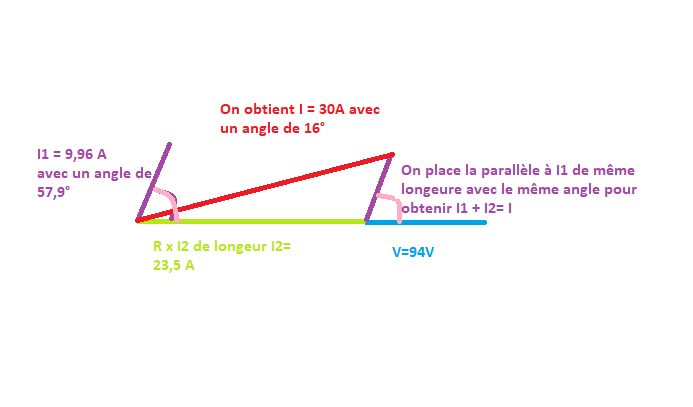
Bien penser à faire une échelle, ici j’ai pris 1 carreau = 2 A et 1 carreau = 10 V
Se muni d’un rapporteur et d’une règle
On mesure 7,5cm en rouge : petit produit en croix : 1carreau = 0,5 cm -> 2 A
donc 7,5 cm = 30 A .
Et voilà on a encore prouvé en quelque étape qu’il est simple de résoudre un exercice d’énergie avec la méthode de Fresnel.